Introduction to Cache Oblivious AlgorithmsPermalink

Cache oblivious algorithms are the algorithms that performs well even when they are not aware of the caching model.

The Cache ModelPermalink

We assume two level memory: cache and main memory. The block size is $B$. The size of the cache is $M$. The size of main memory is assume infinte. If we want to access some data that is not in the cache, we need to pull the whole block that contains the data to the cache first. And we might kick something else and we need to write it back to memory.

1. Accesses to cache are free, but we still care about the computation time (work) of the algorithm itself.
2. If we have an array, it might not be aligned with the blocks. So it will be some extra things at the beginning and the end that doesn’t consume a whole block but we need the extra 2 blocks.
3. Count block memory transfers between cache and main memory. (number of block read/write) Memory Transfer $MT(N)$ is a function of $N$, but $B$, $M$ are parameters and does matter.

Cache Oblivious AlgorithmPermalink

• Algorithms don’t know $B$ and $M$
• Accessing memory automatically fetch block into memory & kick the block that will be used furthest in the future (idealized model)
• Memory is one big array and is divided into blocks of size $B$

Note: if the algorithm is cache oblivious and is efficient in the 2-level model, it will be efficient for k-level model (L1, L2, L3, … caches)

Basic AlgorithmsPermalink

• Single Scanning

  Scanning(A, N)
    for i from 0 to N
        visit A[i]
  

  e.g. sum array.

$MT(N)=\frac{N}{B}+2=O(\frac{N}{B}+1)$ For +2, see the second point in the cache model.

• $O(1)$ parallel scans

  reverse(A,N)
    for i from 0 to N/2
        exchange A[i] with A[N-i+1]
  

  Assuming $\frac{M}{B}>=2,\ MT(N)=O(\frac{N}{B}+1)$

• Binary Search We hope to get $\log_BN=\log N/\log B$, but actually it is $\log(\frac{N}{B})=\log N-\log B$ (At first each access corresponding to one block. At the very last few search they are in the same block)

Divide and ConquerPermalink

• Algorithm divides problem into $O(1)$ case
• Analysis considers point at which the problem
  • fits in cache ($<=M$)
  • fits in $O(1)$ block ($O(B)$)

Order Statistics (median finding)Permalink

• Conceptually partition the array into $N/5$ 5-tuples
• Compute the medium of each one ($MT(N)=O(\frac{N}{B}+1)$)
• Recursively compute median $x$ of these medians ($MT(N)=O(N/5)$)
• Partition around $x$ ($MT(N)=O(\frac{N}{B}+1)$)
• Recurse in one side ($MT(N)=O(7N/10)\approx O(3N/4)$)

  AnalysisPermalink

  $MT(N)=MT(N/5)+MT(3N/4)+O(\frac{N}{B}+1)$

If we assume $MT(1)=O(1)$, see what we get ($L(N)$ is the number of leaves of recurssion tree):

Now we assume $MT(B)=O(1)$, then number of leaves is $(\frac{N}{B})^{\alpha}=O(\frac{N}{B})$

Matrix MultiplicationPermalink

Standard, Naive WayPermalink

$C=AB$ Assume that $A$ is row-major, $B$ is col-major, $C$ is row-major (best possible memory layout)

$O(\frac{N}{B})$ to compute $C_{ij}$ so total $O(N^3/B)$

Black AlgorithmPermalink

Recursively divide the matrix into 4 parts, each is $N/2\times N/2$

We assume we store matrices recursively block. So:

So we stop the recursion tree at the base case, the number of leaves is $O((N/\sqrt{M})^3)$

So the total is

Static Search Tree (Binary Search)Permalink

Goal: $\log_BN$

• Store %N% elements in order in a complete binary tree on %N% nodes
• Cut the tree in the middle level of edges so so that the each part has height $(\log N)/2$ and the upper part has $2^{(\log N)/2}$ nodes which is $sqrt{N}$, and there are $\sqrt{N}$ subtrees at the bottom, each of which has size $\sqrt{N}$. So there are $\sqrt{N}+1$ subtrees in total.
• Recursively layout $\sqrt{N}+1$ subtrees and concatenate

e.g. the index label is the order that is stored in the array.

            1
     2             3
  4     7     10       13
5   6 8   9 11  12   14  15

Analysis: $O(\log{B}N)$ memory transfersPermalink

• consider recursive level of detail at which the size of each subtree $<=B$, so the height of the subtree $>=\log B$
• root-to-node path visits $<=\log N/((\log B)/2)$ subtrees
• each subtree is in at most $2$ blocks
• So the number of memory transfers $<=4\log_BN=O(\log_BN)$
• There exist a dynamic type of this data structure, which can do insert and delete in $O(\log_BN)$ time, but it is super complicated

Cache aware sortingPermalink

• repeated insertion into B-tree, $MT(N)=O(N\log_BN)$ really bad!!! even worse than random access!!! which is $O(N)$
• binary merge sort

• $\frac{M}{B}$-way merge sort
  • divide into $\frac{M}{B}$ subarrays
  • recursively sort each subarray
  • merge: using 1 cache block per subarray

Cache Oblivious SortingPermalink

Actually need an assumption of the cache:

e.g. $M>=B^2$

Use $N^{\epsilon}$-way mergesrot

K-funnelPermalink

It merges k sorted lists of total size $>=\Theta(k^3)$ using $O(k^3/B\log_{\frac{M}{B}}k^3/B+k)$ memory transfers

So we have now Funnelsort. use $k=N^{1/3}$

• divide array into $N^{1/3}$ equal segments
• recursively sort each
• merge using $N^{1/3}$-funnel

So as long as it is not in the base case, $\frac{N}{B}\centerdot\log_{\frac{M}{B}}(\frac{N}{B})$ dominates $N^{1/3}$

Revisit K-funnelPermalink

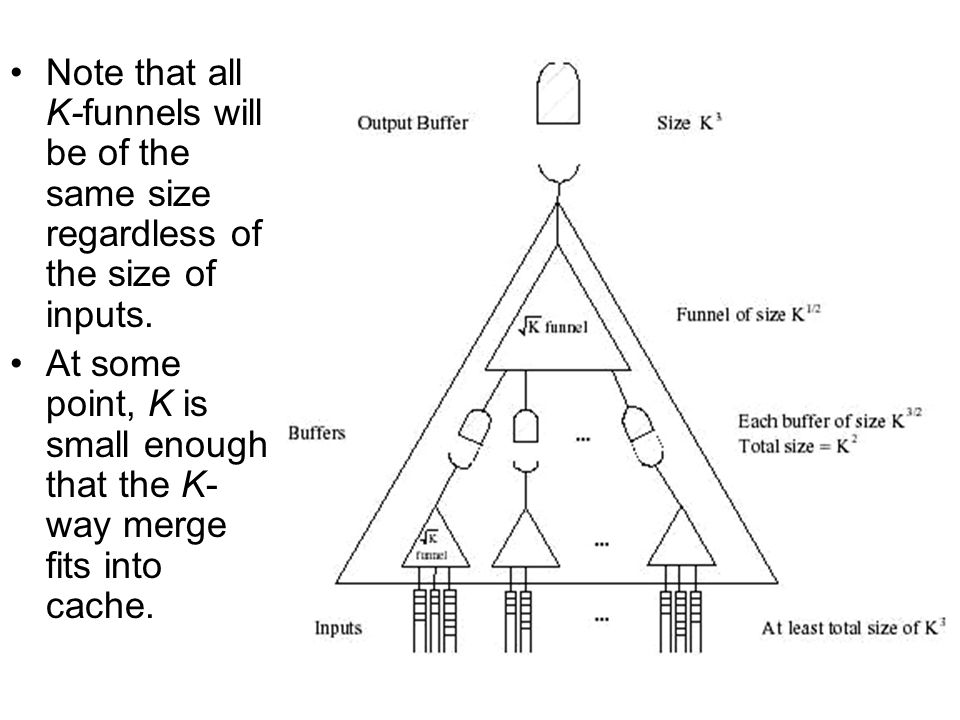
First take a look at space excluding input and output buffers

So merge means to fill up the top buffer

• merge two children buffer as long as they both are non-empty
• whenever one empties, recursively fill it
• at leaves, read from input list

Analysis:

• consider first recursive level of detail, J, at which evey J-funnel fits 1/4 of the cache (It means $cJ^2<=M/4$)
• can also fit one block per input buffer (of J-funnel)

• swapping in (reading J-funnel and one block per input buffer) ($O(\frac{J^2}{B}+J)=O(J^3/B$)
• when input buffer empties, swap out and recursively fill and swap back in. Swapping back in cost $O(J^3/B)$
• charge cost to elements that fill the buffer (amortize analysis)
• $J^3$ such elements
• number of charges of $O(1/B)$ cost to each elements is $\log K/\log J=\Theta(\log K/\log M)$

So the total cost is

assuming