Some Notes about Fibonacci HeapsPermalink

Operations:Permalink

• make_heap Return an empty heap
• insert(i,h) Add item $i$ to heap $h$.
• find_min(h) Return the smallest item in heap $h$
• delete_min(h) Delete min from heap $h$ and return it
• meld(h1, h2) Return the heap formed by putting all elements in $h_1$ with all the elements in $h_2$. $h_1$ and $h_2$ are destroyed.
• decrease_key(delta, i, h) Assume that position of $i$ is known. Decrease the value of item $i$ of delta (delta > 0)
• delete(i, h) Assume that position of $i$ is known. Delete $i$ from heap

Amortized Time ComplexityPermalink

• delete_min(h) and delete(i, h) takes $O\left(\log n\right)$ time
• Other operations take $O\left(1\right)$ time

StructurePermalink

• Heap Ordered Trees: Rooted tree containing a set of item, 1 item / node, with items arranged in heap order
• Heap Order: Key of item $x$ is no less than the key of the item in its parent $p\left(x\right)$, provided $x$ has a parent.
• Linking: Combine two item-disjoint trees into one. (Make one root (bigger) a child of the other (smaller))
• Fibonacci heap (F-heap): Collection item disjoint heap ordered trees. (the algorithms impose an additinoal constraint).
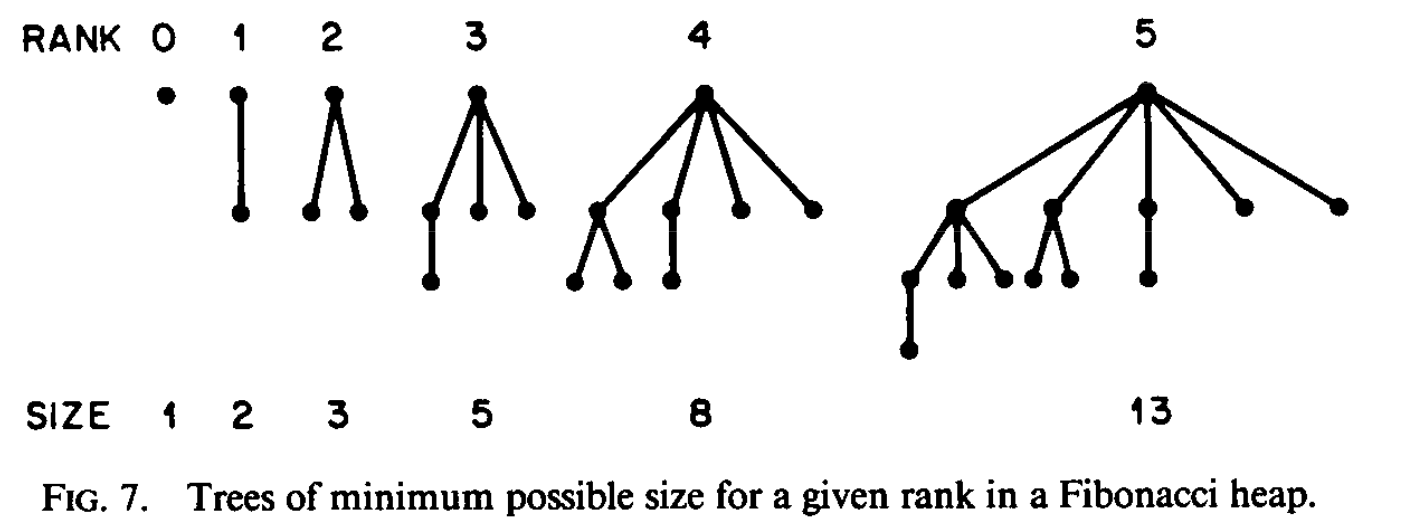
• rank $r\left(x\right)$: Number of children of node $x$. It turns out that if $x$ has $n$ descendants, the number of children is at most $\log n$.
• Nodes will be marked or unmarked.

Representation of F-HeapPermalink

• Each node contains pointer to its parent (or to $null$ if it doesn’t have one).
• Each node has a pointer to one of its children (or to $null$ if it doesn’t have any).
• The children of each node are in a doubly linked circular list.
• Node has its rank $r\left(x\right)$ and a bit indicating its mark.
• All the roots of the (sub)heaps are in a circular list.
• There is a pointer to a root containing an item of minimum key ($minimumnode$ of the F-heap).

DefinitionsPermalink

• $S$: Collection of Heaps.
• $\Phi \left(S\right)$: Potential of $S$.
• $m$ operations with times $t_1,t_2,\cdots ,t_m$
• $a_i$ amortized time for operation $i$.
• ${\Phi }_i$: Potential after operation $i$.
• ${\Phi }_0$: Initial potential.
• $\sum t_i=\sum (a_i-{\Phi }_i+{\Phi }_{i-1})={\Phi }_0-{\Phi }_m+\sum a_i$
• ${\Phi }_0$ is initially zero.
• ${\Phi }_i$ is non-negative.

IdeaPermalink

• Potential of a collection of heaps: The total number of trees they contain.
• Initial potential is zero
• make_heap, find_min, insert, and meld take $O\left(1\right)$ time.
• Insertion increases the number of trees by one. And other operations do not affect the number of trees
• delete_min: Amorzied time $O\left(\log n\right)$ where $n$ is the number of items in the heap. Increases the number of trees by at most $\log n$.
• Linking Step: Decreases the number of trees by one.

Implementation of OperationsPermalink

• make_heap Just retur $null$
• find_min(h) Return the minimum node of $h$
• insert(i, h) Create a heap of only node $i$ and replace $h$ by meld of $h$ and the new heap
• meld(h1, h2) Combine the root lists of $h_1$ and $h_2$ into one list and set the minimum node to the appropriate new minimum node.

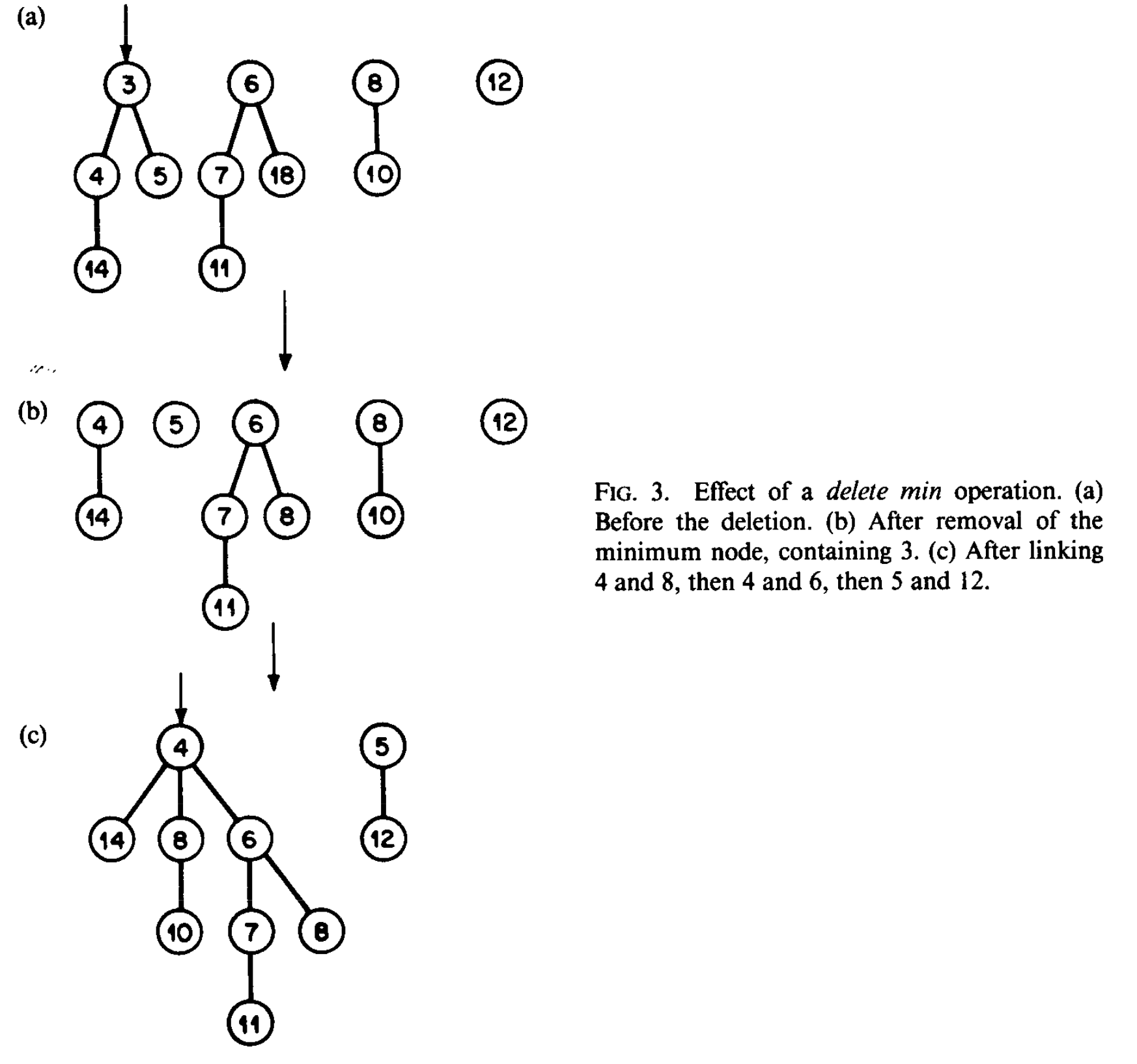
delete_min(h)Permalink

• Remove the minimum node ($x$) from $h$
• Concatenate the list of children of $x$ with the list of roots of $h$ (other than $x$)
• Repeat the following Linking Step until it no longer applies
  • Find any two trees whose roots have the same rank and link them (the new root has rank +1)
• Form a list of the remaining roots.
• Find the item of minimum key.

Note: Implementation (use an array indexed by ranks).

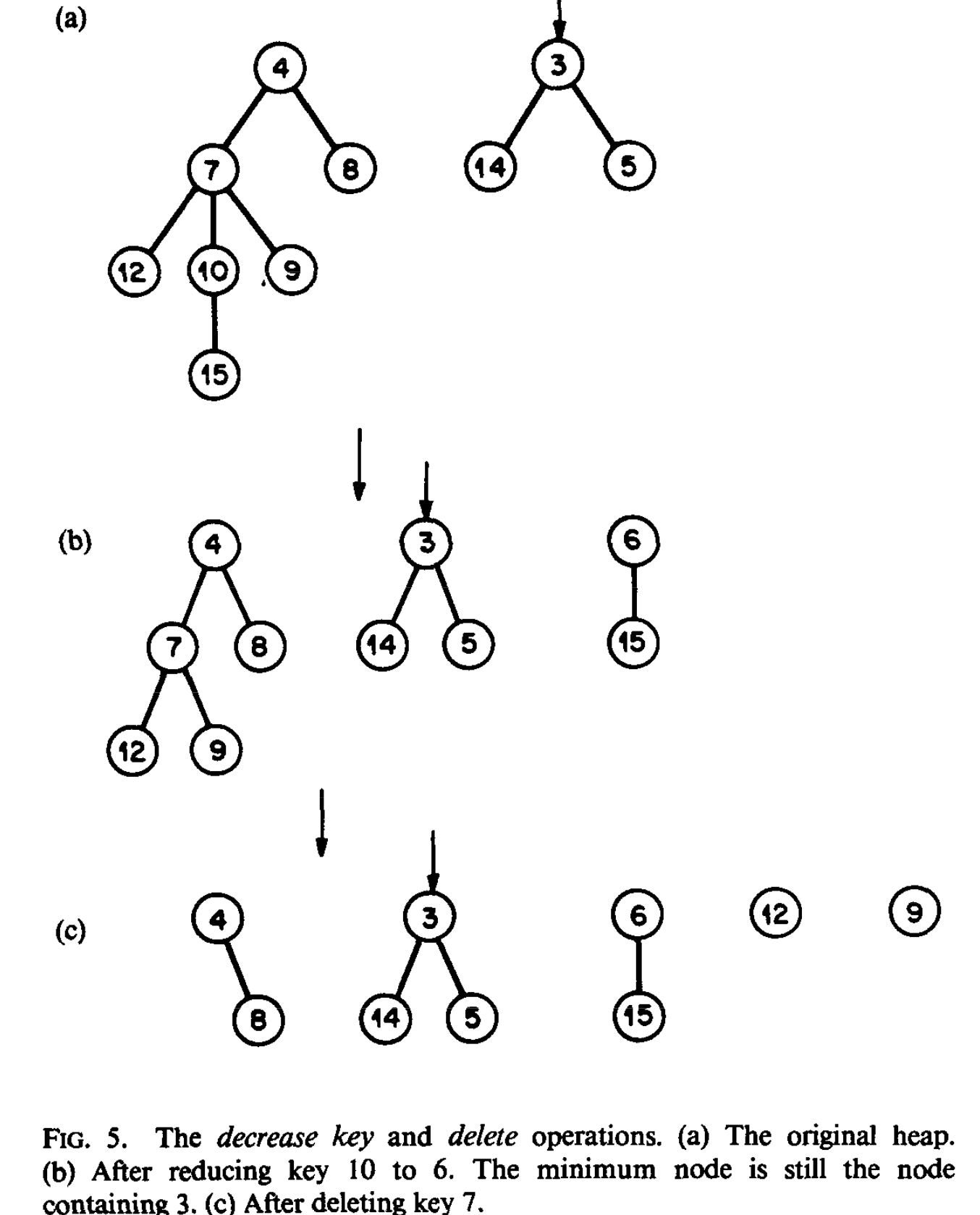
decrease_key(delta, i, h)Permalink

• Key of item $i$ is decreased by delta
• Cut out the node $x$ containing item $i$ from its parent
• $x$ and its descendants is added as a new tree of $h$.
• The appropriate update operations are performed

delete(i, h)Permalink

• Find node $x$ containing item $i$.
• Cut out the node $x$ containing item $i$ from its parent.
• Form a new list of roots by concatenating the list of children of $x$ with the original list of roots.
• The appropriate update operations are performed.
• delete takes $O\left(1\right)$, except when the minimum element is deleted.

Additional Details (Cascade Cut)Permalink

• When node $x$ has been made a child of another node by a linking step and it loses 2 of its children through cuts, we cut the edge joining $x$ and its parent and we make $x$ ad new root (as in decrease_key)
• A decrease_key or delete operation my casue a possibly large number of cascading cuts.

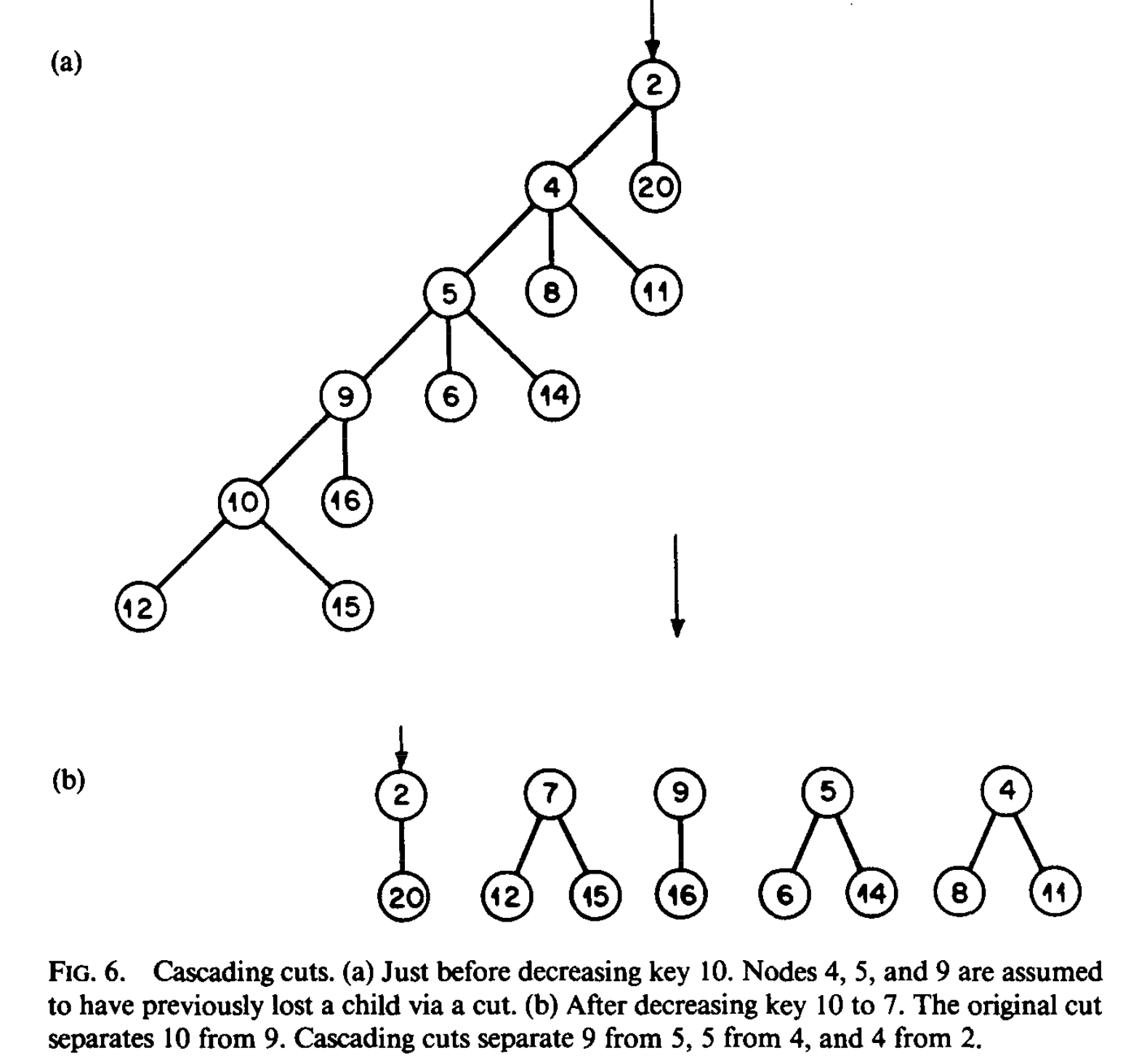
Marking NodesPermalink

• Purpose: Keep track of where to make cascade cuts.
• Unmark $x$: When making a root node $x$ a child of another node in a linking step
• When curring edge joining $x$ and its parent $\left(p\right(x\left)\right)$, we decrease the rank of $p\left(x\right)$ and check it $p\left(x\right)$ is a root
  • if $p\left(x\right)$ is not a root, we mark it if it is unmarked and cut the edge to its parent it it is marked. (latter cut my be cascading)
• Each cut takes $O\left(1\right)$.

Crucial PropertiesPermalink

1. Each tree in an F-heap has a size at lease exponential in the rank of its root. i.e. the number of children is at most $\log n$.
2. The number of cascading cutus that take place during a sequence of heap operations is bounded by the number of decrease key and delete operations.

ObservationsPermalink

• The purpose of cascade cuts in to preserve property 1.
• Loss of two children rule limits the frequency of cascade cuts.

Lemma 1: Let $x$ be any node in a F-heap. Arrange the children of $x$ in the order they were linked to $x$, from earliest to latest. Then the $i^{th}$ child of $x$ has rank of at least $i-2$.

Corollary 1: A node of rank $k$ in an F-heap has at least $F_{k+2}\ge {\varphi }^k$ descendants, including itself, where $F_k$ is the $k^{th}$ Fibonacci number and $\varphi$ is the golden ratio.

RedefinitionPermalink

• Potential: Total numbere of trees plus twice the number of marked nonroot nodes.
• The bounds of $O\left(1\right)$ for make_heap, find_min, insert, and meld remain valid, as does not $O\left(\log n\right)$ bound for delete_min.
• delete_min(h): increases the potential by at most $1.4404\log n$ minus the number of linking steps, since, if the minimum node has rank $k$, then ${\varphi }_k\le n$ and thus

Revist decrease_keyPermalink

• Causes potential to increase by at most three mins the number of cascading cuts, since
  • the first cut converts a possible unmarked nonroot node into a root
  • each cascading cut converts a marked nonroot node into a root
  • the last cut can convert a nonroot node from unmarked to marked
• It follows that decrease key has an $O\left(1\right)$ amortized time bound.

Revist deletePermalink

Just combine the analysis of decrease_key with delete_min

SummaryPermalink

If we begin with no F-heaps and perform an arbitrary sequence of F-heap operations, then the total time is at most the total amortized time, where the amortized time is $O\left(\log n\right)$ for each delete_min or delete, and $O\left(1\right)$ for each other operations.